Tercera contrarréplica a Rolando Astarita a propósito del problema de la transformación de Marx

Conforme un debate se alarga, van apareciendo cuestiones adyacentes al asunto original que motivó el debate. En ocasiones se trata de una estrategia deliberada de alguno de los debatientes (abrir nuevos temas sin cesar para no afrontar el fondo de las críticas que se le han planteado) y en otras ocasiones es una mera consecuencia del desarrollo desordenado (no moderado) del debate. Dado que estoy seguro de que Rolando Astarita no busca desviar el debate de la cuestión original –si Moseley resuelve adecuadamente el problema de la transformación de Marx o no–, permítaseme que me centre en responder a aquellos argumentos del nuevo post de Astarita que realmente tratan esa cuestión y no otras que, acaso tengan interés teórico, pero que nos alejan del asunto central de este debate.

Mi crítica a Moseley es muy sencilla: su solución al problema de la transformación consiste en presuponer que los capitalistas adquieren el capital constante y el capital variable no a sus valores, sino a sus precios de producción. Basta, pues, con que Moseley nos muestre que existe equilibrio interdepartamental a unos precios de producción que igualan la tasa de ganancia en todos los sectores para que el problema de la transformación quede satisfactoriamente resuelto. Pero, como ya expliqué en Anti-Marx y he reiterado en los posts anteriores, hay un agujero en esta lógica: si la tasa general de ganancia cambia, el equilibrio interdepartamental anterior desaparece y sólo podemos reestablecerlo a unos nuevos precios de producción que, en agregado, no son iguales a sus valores (a sus valores agregados) o, alternativamente, a una masa de ganancia que, en agregado, no es igual a la masa de plusvalía. Por tanto, el problema de la transformación (cómo pasar de valores a precios de producción manteniendo la doble igualdad agregada entre valores y precios y entre plusvalía y ganancia) se mantiene.

Astarita no consigue solucionar este problema básico. No basta con decir, como él mismo repite, que Moseley ha demostrado que “no hay que transformar los precios de los insumos”: pues cuando hay un cambio en la tasa general de ganancia, sí que hay que (re)calcular los nuevos precios de producción de los insumos y, a esos nuevos precios de producción, el agregado de valores (que no se han visto modificados) no coincide con el agregado de precios de producción. Esto es algo que el propio Astarita reconoce. Véase:

El valor agregado debe entonces reponer el capital variable y añadir la plusvalía. En consecuencia, la igualdad entre valor agregado y salarios más beneficios no es un tema de simple preferencia para resolver un sistema de ecuaciones a lo Bortkiewicz, sino el resultado de la forma en que opera el capitalismo.

(…)

Cuando los precios de producción deben obtenerse por distribución de masas de valor, y por lo tanto, cuando todo lo que en algún lugar se restó debe reaparecer en otro lugar, la suma de los valores es igual a la suma de los precios de producción, pero la suma de la masa de plusvalía no puede ser igual a la suma de las ganancias. Alternativamente, si estas últimas son iguales, a través de los períodos de producción la suma de los valores no puede ser igual a la suma de los precios de producción

(…)

Tenemos la igualdad en el valor nuevo añadido en cada ronda. Si el número de obreros se mantiene, y se mantiene la duración e intensidad de la jornada de trabajo, el valor global añadido por el trabajo no se modifica. Suponiendo que el salario se mantiene constante, se modifica la distribución del beneficio entre las ramas, y en consecuencia los precios de producción y la tasa de beneficio.

(…)

Las dos igualdades agregadas son satisfechas dentro de cada período porque, dentro de un período, cuanto más bajo sea C se reducen el precio-valor y los precios de producción por el mismo monto. Entre períodos la igualdad agregada de precio no será satisfecha porque C cambia entre períodos

Es decir, que el propio Astarita admite que la única igualdad agregada que es capaz de mantener la solución de Moseley es “salarios agregados+plusvalía agregada” y “salarios agregados+ganancia agregada”. Pero ésa no es la igualdad agregada que exige Marx para resolver el problema de la transformación. Marx exige que C+V+P=C+V+G, a saber, que la totalidad del valor agregado (no sólo el valor añadido agregado) sea igual a los precios de producción agregados. Vuelvo a repetir, resaltando los extractos clave en negrita:

La suma de los precios de producción de todas las mercancías fabricadas en la sociedad en su conjunto —considerando todas las ramas de producción— es igual a la suma de sus valores (C3, 9, 259).

La suma de todos los beneficios de todas las esferas de producción ha de ser igual a la suma de la plusvalía, y la suma de los precios de producción de todo el producto social ha de ser igual a la suma de su valor (C3, 10, 273).

Si Astarita reconoce ahora que esa doble igualdad agregada no existe ni puede existir, entonces está admitiendo que Moseley no ha resuelto el problema de la transformación. No debería haber mucha más discusión llegados a este punto dado que, a confesión de parte, relevo de pruebas.

Sin embargo, Astarita trata de convencernos de que, aun cuando los nuevos precios de producción agregados no coincidan con los antiguos valores agregados entre distintos períodos de tiempo, éstos sí coinciden dentro del mismo período. En otras palabras, lo que ha ocurrido es que la expresión cuantitativa de esos valores agregados ha cambiado entre períodos a pesar de que el tiempo de trabajo social no lo haya hecho. Por ejemplo, imaginemos que, en t=1, el valor agregado se expresa en 960 onzas y los precios de producción agregados también 960 onzas; si en t=2, los precios de producción agregados caen a 930 onzas, Astarita nos asegura que eso se deba a que la expresión social de esos valores agregados también se han reducido a 930 onzas aun cuando el tiempo de trabajo social no haya variado en nada. Por dogmática definición, los valores agregados siempre coinciden con los precios de producción agregados dentro de cada período aun cuando haya evidentes discrepancias cuantitativas entre períodos.

Por tanto, y por resumir, aquello de lo que nos intenta convencer Astarita es de que:

1. Entre períodos de tiempo, la suma del capital variable agregado y de la plusvalía agregada se mantiene constante (si no hay cambios en el tiempo de trabajo socialmente necesarios).

2. Dentro de un mismo período, los valores agregados coinciden con los precios de producción agregados y la plusvalía agregada coincide con la ganancia agregada. Pero entre períodos sólo se dará esa coincidencia en supuestos excepcionales.

En la siguiente sección vamos a demostrar que, aun cuando la expresión social del valor agregado de las mercancías no cambie entre períodos, los precios de producción agregados sí cambian entre períodos y, por tanto, la igualdad entre valores agregados y precios de producción agregados no se cumple ni entre períodos ni dentro de un mismo período.

Un ejemplo de desigualdad entre valores y precios de producción dentro de un mismo período de tiempo

Para demostrar que valores y precios de producción no coinciden, en la solución que formula Moseley, ni siquiera dentro de un mismo período, vamos a partir de un ejemplo que nos expone Astarita cuando desarrolla el argumento de Mario Cogoy de por qué la doble igualdad agregada (tal como hemos venido señalando reiteradamente) no puede cumplirse salvo en supuestos excepcionales. Las directrices de ese ejemplo de Astarita (expuestas en su apartado “las dificultades de transformar simultáneamente insumos y outputs, una explicación con sabor sraffiano”) son las siguientes: tenemos una economía donde se produce hierro y trigo, donde la composición orgánica del trigo es superior a la del hierro, donde las tasas de plusvalía son idénticas entre sectores y donde la proporción material entre el hierro y el trigo dentro de la masa de plusvalía no coincide con su proporción dentro del capital agregado. Pues bien, en términos físicos, una economía que encajaría con las directrices que nos da Astarita sería la que aparece en la tabla I (añadimos un sector adicional, el sector III, donde se produce oro para que éste nos sirva de numerario):

Si el tiempo de trabajo social es de 12 horas de trabajo por tonelada de hierro, 4 horas de trabajo por tonelada de trigo y 1 hora de trabajo por onza de oro, podremos expresar las mercancías anteriores en valores tal como hacemos en la tabla II:

Respecto a la tabla II, démonos cuenta de tres cosas. Primero, como hemos supuesto que una hora de trabajo social es igual a una onza de oro, podemos expresar la tabla II en forma de onzas de oro y esas onzas de oro serán un reflejo de las horas de trabajo social. Segundo, las tablas I y II cumplen con los requisitos que exponía Astarita: la composición orgánica del capital del trigo es superior a la del hierro, las tasas de plusvalía son idénticas entre sectores y la proporción entre trigo y hierro dentro del capital social agregado (30 toneladas de hierro versus 90 toneladas de trigo, esto es, una proporción de 1:3) no es la misma que en el plusproducto agregado (4,16 toneladas de hierro versus 17,5 toneladas de trigo, esto es una proporción 1:4,2). Y tercero, la tabla II no deja de ser una versión extendida de la tabla original con la que Moseley arranca su exposición sobre cómo solucionar el problema de la transformación y que reproducimos ahora como Tabla A:

Y es que si, en nuestra tabla II, agregamos C1+C2 e incluimos el departamento III dentro del departamento I, tendríamos la siguiente tabla III que es exactamente la misma que la tabla A anterior (salvo porque su sector I es nuestro sector II y viceversa):

Por consiguiente, podemos transformar en precios de producción los valores que aparecen en la tabla II tal como Moseley transforma en precios de producción los valores que aparecen en la tabla A. A saber:

En esta tabla IV, la tasa general de ganancia ya es la misma en todos los sectores de la economía (33,3%) y existe equilibrio interdepartamental: el hierro producido por el departamento I se vende y se compra por 360 onzas de oro (C1); el trigo producido por el departamento II se vende y se compra por 480 onzas de oro (C2+V más parte de P) y el oro producido por el departamento III se compra y se vende por 120 onzas. Nuevamente, nuestra tabla IV no es más que una versión extendida de la tabla de precios de producción que presenta Moseley y que denominamos ahora tabla B:

Y es que, si nuevamente sumamos C1+C2 e incluimos el departamento III dentro del departamento I, obtendremos la tabla V que es exactamente la misma que la tabla B:

En el ejemplo que utiliza Moseley, la transformación de valores en precios de producción sí respeta la doble igualdad agregada entre valores-precios de producción y masa de plusvalía-masa de ganancia, pero Astarita nos dirá que ello ocurre porque nos hallamos dentro de un mismo período temporal (los precios de producción de la tabla IV son sólo la expresión social de los valores de la tabla III en un determinado momento económico). Pues bien, analicemos ahora qué sucederá si, como expongo en Anti-Marx, los salarios se incrementan en un 20%. Empecemos por los cambios en la distribución física de la producción social: los salarios (en trigo) de nuestra tabla I se incrementarán en un 20%, dando lugar a la tabla VI:

Como podemos observar, el trigo destinado a abonar el capital variable aumenta de 60 a 72 toneladas y, en consecuencia, el plusproducto agregado se reduce desde 4,16 toneladas de hierro y 17,5 toneladas de trigo (tabla I) a 4,16 toneladas de hierro y 5,5 toneladas de trigo. Si el tiempo de trabajo socialmente necesario para producir el hierro sigue siendo de 12 horas por tonelada, el socialmente necesario para producir el trigo sigue siendo de 4 horas por tonelada y el socialmente necesario para producir el oro sigue siendo de 1 hora por onza, pasaremos a la tabla VII:

La tabla VII refleja la tabla en valores tras los cambios en la distribución salarial: se trata del equivalente a nuestra tabla II (o a la tabla A del propio Moseley) a los nuevos salarios (20% superiores en términos de trigo pero también 20% superiores en onzas de oro, es decir, en valores). Vemos por consiguiente que, en contra de lo que sostiene Astarita, tras el cambio en los salarios no ha habido ningún cambio en el valor agregado dentro de esa economía. Y no lo ha habido por el simple hecho de que el tiempo de trabajo social no se ha alterado. El tiempo de trabajo social siguen siendo 960 horas de trabajo social que equivalen a 960 onzas de oro. Repito una vez más: el valor agregado no ha cambiado entre períodos por el hecho de que los salarios hayan cambiado. Antes y después del cambio salarial, el valor agregado es idéntico (960 horas = 960 onzas de oro).

Ahora bien, como ya ocurría en la tabla II, en la tabla VII existe equilibrio interdepartamental (por ejemplo, el hierro debería comprarse por 360 onzas pero se vendería por 410), pero según Moseley esto es irrelevante porque los inputs no se compran y venden a sus valores, sino a sus precios de producción. De modo que tenemos que calcular los precios de producción a los que se efectuarán los intercambios de las mercancías que figuran (en términos físicos y en valores) dentro de las tablas VI y VII (es decir, hemos de calcular el equivalente a nuestra tabla IV o a la tabla B de Moseley). Si hacemos eso, llegaremos a la siguiente tabla VIII:

En la tabla VIII ya existe equilibrio interdepartamental… pero los precios de producción agregados (979,36 onzas) no coinciden con el valor agregado dentro del mismo período (960 onzas en la tabla VII). La plusvalía agregada sí coincide dentro del mismo período (192 onzas en las tablas VII y VIII) y la masa agregada de trabajo vivo (capital variable agregado y plusvalía agregada) coincide dentro del mismo período y entre períodos (480 onzas), pero, repetimos una vez más, valores agregados y precios de producción agregados no coinciden dentro del mismo período. Por consiguiente, lo crucial de este ejemplo es que ilustra que ni siquiera es cierto que la doble igualdad agregada se cumpla dentro del mismo período en la solución de Moseley: la plusvalía agregada sí coincide con la masa de ganancia agregada, pero los precios de producción agregados no coinciden con los valores agregados.

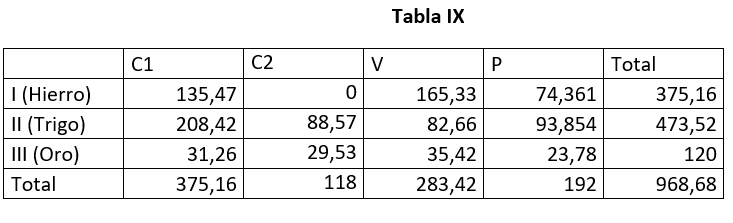
La solución de la tabla VIII no es, empero, la única solución posible (no es la única transformación de la tabla VII susceptible de arrojar un equilibrio interdepartamental). De hecho, la tabla VIII tiene un problema: el departamento III (el productor de oro) no produce realmente 121,41 onzas de oro, sino sólo 120 onzas: no podemos decir que el precio de producción de 120 onzas son 121,41 onzas porque el dinero no tiene precio, es decir, 120 onzas son 120 onzas, sin más (ese desdoblamiento del precio del oro es consecuencia de haber impuesto la restricción de que el trabajo vivo agregado no cambie entre las tablas VII y VIII). Si corregimos este problema y transformamos los valores en precios de producción imponiendo la restricción de que la plusvalía agregada sea igual a la ganancia agregada (192 onzas) y de que el valor monetario de las 120 onzas de oro del departamento III sean 120 onzas de oro, llegaremos a la tabla IX:

En esta tabla IX, 1 onza de oro sigue siendo la expresión social de 1 hora de tiempo de trabajo social (se producen 120 onzas en 120 horas de trabajo social) y, como vemos, ni el valor agregado (960 onzas) coincide con los precios de producción agregados dentro del mismo período (968,68 onzas) ni tampoco el trabajo vivo agregado expresado en valores (480 onzas) coincide con el trabajo vivo agregado expresado en precios de producción (475,42 onzas), ni dentro de un mismo período ni entre períodos. Por tanto no: tal como podemos observar, Moseley no ha resuelto el problema de la transformación de Marx ni siquiera en los propios términos reformulados que pretende establecer Moseley (es decir, que la doble igualdad agregada sólo se ha de dar dentro de cada período y no entre períodos). Y Astarita no sale airoso defendiendo la mala solución de Moseley al problema de la transformación de Marx.

Una última aclaración metodológica

Antes de terminar, querría aclarar cuál es el propósito central de mi crítica a Moseley en Anti-Marx. En contra de lo que señala Astarita, mi crítica a Moseley no tiene que ver con su exposición sobre el proceso específico de cómo el sistema alcanza un nuevo equilibrio. Mi crítica tiene que ver con que, en ese nuevo equilibrio, el valor agregado no coincide con el precio de producción agregado (o la plusvalía agregada no coincide con la ganancia agregada). Eso es lo que criticó Bortkiewicz en su momento y lo que Moseley, con su presunta solución al problema de la transformación, no consigue realmente solventar: pues, como ya hemos demostramos en el post anterior, la única solución de equilibrio que es capaz de alcanzar Moseley ante un cambio en los salarios es la misma solución final que anticipa el método de Bortkiewicz y que, como el propio Bortkiewicz ya expuso respecto a esa solución, no consigue respetar la doble igualdad agregada entre, por un lado, precios de producción y valores y, por otro, plusvalía y ganancia. Astarita parece creer (o pretende hacerle creer a su lector) que mi crítica a Moseley es meramente procedimental, a saber, que no soy capaz de pensar en otro método, distinto al simultáneo de Bortkiewicz, para reestablecer el equilibrio una vez ha sido perturbado. De ser así, bastaría con que Astarita nos mostrara –como pretendió hacer en su primer post– que, a través del método secuencial de Moseley, sí podemos alcanzar un nuevo equilibrio, para que toda mi crítica original quedaría anulada. Pero en Anti-Marx analizo las distintas soluciones al problema de la transformación de Marx, y entre ellas la de Moseley, bajo la siguiente premisa inquisitiva inicial:

Por consiguiente, el reto planteado por Bortkiewicz inflige un duro golpe a la teoría marxista: o bien los precios de producción no reflejan los valores o bien la ganancia no es la distribución de la plusvalía. O bien, por tanto, los precios de producción son algo distinto a una exteriorización de los valores, o bien el beneficio es algo distinto a una exteriorización de la plusvalía.

No sólo eso, justo antes de exponer la solución específica de Moseley, reflexiono sobre el método iterativo de Shaikh que, tras diversas rondas de ajuste, conduce dinámicamente al mismo equilibrio final que anticipa con sus ecuaciones simultáneas Bortkiewicz. No es, por tanto, que no conciba cómo puede pasarse de una situación de desequilibrio a una situación de equilibrio sin recurrir al método simultáneo de Bortkiewicz: es que los métodos dinámicos –de Shaikh o de Moseley– sólo arrojan misma la solución final de Bortkiewicz y esa solución no es válida. Tal como señalo en el libro respecto a la solución iterativa de Shaikh:

Tras varias rondas de reajustes, el precio de los inputs y el de los outputs [en el método iterativo de Shaikh] coincide con la solución simultaneísta proporcionada por Bortkiewicz, es decir, el multiplicador termina convergiendo a 1 (en la Tabla 5.12)

Y respecto a la invalidez de la solución de Shaikh añado a renglón seguido del párrafo (y justo antes de pasar a examinar la alternativa de Moseley):

El problema de la solución de Shaikh es que, si bien el valor agregado del capital mercantil coincide en cada período con el valor agregado de los precios de producción (875 onzas), la plusvalía agregada jamás coincide con la masa de ganancia agregada: incluso en la última ronda de ajustes, la masa de ganancia agregada es de 175 onzas cuando la plusvalía agregada era de 200 onzas. Por tanto, no es una solución que solvente plenamente el problema de la transformación bajo las premisas expuestas por Marx.

En tercer lugar, podemos mencionar la solución de Fred Moseley (2016)…

Es decir, y como ya dije, Bortkiewicz nos muestra la solución final de equilibrio del sistema y Shaikh o Moseley (cada uno con sus distintos supuestos de partida) sólo nos indican la trayectoria que nos conduce a esa solución de equilibrio de Bortkiewicz. Pero, repito, el problema esencial no es que Moseley (o Shaikh) sea incapaz de explicar el proceso de reequilibrio, sino que su solución –que, como resultado final, es la misma que la de Bortkiewicz– no respeta la doble igualdad agregada entre, por un lado, valores y precios de producción y, por otro, plusvalía y ganancia (en el libro, calculo el nuevo equilibrio de Moseley manteniendo constante el valor agregado, de modo que lo que no coincide es la plusvalía agregada con la ganancia agregada, pero en éste y en post anterior ya demostré que, si la plusvalía agregada coincide con la ganancia agregada dentro de la solución de Moseley, el valor agregado no coincide con los precios de producción agregados).

En definitiva, Astarita sigue sin probar que la solución de Moseley al problema de la transformación de Marx sea correcta. La plusvalía agregada coincide con la ganancia agregada a costa de que los valores agregados no coincidan con los precios de producción agregados: no ya entre períodos sino tampoco dentro de cada período.