Cuarta contrarréplica a Rolando Astarita a propósito del problema de la transformación de Marx
Astarita ha vuelvo a replicar, por cuarta vez, a mi anterior contrarréplica. En este caso, me temo que no hay argumentos nuevos por su parte sino una mera pretensión de evitar responder a las nuevas críticas que se contenían en mi anterior contrarréplica. En aras de la claridad, vamos a resumir los puntos principales del debate.
Primero, mi argumento expuesto en Anti-Marx (al que Astarita pretende replicar) es el siguiente:
La solución al problema de la transformación de Marx requiere que se cumpla la doble igualdad agregada entre “suma de valores=suma de precios de producción” y “masa de plusvalía=masa de ganancia”.
Moseley aparentemente logra mantener esa doble igualdad agregada suponiendo que los inputs se adquieren a sus precios de producción.
Pero cuando introducimos un cambio de variables dentro del ejemplo de Moseley (verbirgracia, un aumento de los salarios) y se hace necesario transitar hacia un nuevo equilibrio (aunque se transite mediante un método secuencial que muestre todas las distintas etapas del desequilibrio), la doble igualdad agregada deja de respetarse.
Por tanto, Moseley no logra solucionar el problema de la transformación de Marx.
Por su parte, Astarita ha contraargumentado que Moseley sí logra solventar el problema de la transformación de Marx porque:
Entre períodos de tiempo, la suma del capital variable agregado y de la plusvalía agregada se mantiene constante (si no hay cambios en el tiempo de trabajo socialmente necesarios).
Dentro de un mismo período, la suma de los valores coincide con la suma de los precios de producción y la plusvalía agregada coincide con la ganancia agregada. Pero entre períodos sólo se dará esa coincidencia en supuestos excepcionales.
A este contraargumento de Astarita, se le pueden efectuar dos réplicas (que son las que narro en mi post anterior):
Marx sí expone claramente la necesidad de que se respete en todo momento la igualdad entre la suma de valores y la suma de precios de producción, es decir, C+V+S=C+V+P. Cuando Astarita nos dice que, entre períodos de tiempo, sólo es necesario que se mantenga la igualdad V+S=V+P, Astarita está contradiciendo a Marx. La evidencia textual de Marx avala que C+V+S deba ser igual a C+V+P y, como veremos a continuación, Astarita ni siquiera disputa esa evidencia textual.
En la solución que nos ofrecen Astarita y Moseley, ni siquiera se tiene por qué respetar la doble igualdad agregada dentro de un mismo período de tiempo. Esto lo demostré en mi post anterior utilizando un ejemplo numérico inspirado en los propios argumentos de Astarita: en ese ejemplo numérico puse de manifiesto cómo unas relaciones físicas de producción (de trigo, hierro y oro) podían dar lugar a las mismas relaciones de valores de Astarita y Moseley y cómo esas relaciones de valores, aun manteniéndose invariantes entre distintos momentos del tiempo (la suma de valores no cambiaba entre períodos de tiempo), arrojaban unos precios de producción agregados que sí variaban entre distintos momentos del tiempo (de modo que la suma de valores no coincidía con la suma de precios de producción ni siquiera dentro de cada período temporal).
¿Qué tiene que decir Astarita respecto a estas dos réplicas? Lo vamos a explorar en los dos siguientes epígrafes. Y, una vez concluidos esos dos primeros epígrafes, efectuaré una serie de comentarios auxiliares y secundarios que en cierto modo se desvían de este argumento central pero que, al parecer, Astarita considera indispensables para no “evadir” sus argumentos.
De la solución al problema de la transformación a la validez de la ley del valor
Por solución al problema de la transformación nos referimos a demostrar que la ley del valor sigue operando a través de los precios de producción a pesar de que éstos diverjan cuantitativamente de aquéllos. En esencia, se trata de resolver esta aparente contradicción que el propio Marx reconoce:
[Con los precios de producción,] la teoría del valor, pues, parecería ser incompatible con el movimiento real y con el fenómeno real de la producción, de modo que deberíamos abandonar toda esperanza de entender estos fenómenos (C3, 8, 252).
Y, como también hemos expuesto, la solución que ofrece Marx al problema de la transformación consiste en requerir que se cumplan dos condiciones (en realidad, como ya expusimos en un post anterior, tres): la suma de valores es igual a la suma de precios de producción; la suma de las plusvalías es igual a la suma de las ganancias. Así lo relata Marx:
La suma de todos los beneficios de todas las esferas de producción ha de ser igual a la suma de la plusvalía, y la suma de los precios de producción de todo el producto social ha de ser igual a la suma de su valor (C3, 10, 273).
O alternativamente:
En conjunto, las mercancías se venden 2 +7 + 17 = 26 por encima de su valor y -8 — 18 = 26 por debajo de su valor, de manera que las divergencias entre el precio y el valor se cancelan entre sí cuando la plusvalía es distribuida proporcionalmente, esto es, añadiendo una ganancia media del 22 % sobre un capital adelantado de 100 en los precios de coste de las mercancías producidas en los sectores I-V. Un grupo de mercancías se vende por encima de sus valores en la misma medida en que otro grupo se vende por debajo (C3, 9, 257).
Pero, como hemos venido mostrando a lo largo de este debate, esa doble igualdad agregada (valores-precios de producción y plusvalía-ganancia) no tiene por qué cumplirse: de hecho, como el propio Astarita ha reconocido, sólo se cumplirá en circunstancias extraordinarias. En su última réplica, Astarita nos dice que “si Marx hubiera aplicado un esquema de reproducción (los outputs de una rama son insumos en la otra) probablemente hubiera tenido que cambiar el esquema numérico. Y entonces hubiera surgido la posibilidad de discrepancias entre suma de precios de producción y suma de valores cuando ocurren reajustes ocasionados por variaciones en la distribución del valor agregado”. Por tanto, lo que está señalando Astarita es que si Marx hubiese estudiado el problema de la transformación dentro del análisis del equilibrio interdepartamental, se habría visto forzado a reconocer que la suma de valores no puede coincidir con la suma de precios de producción. A saber, que Marx se habría visto forzado a reconocer que su solución al problema de la transformación (la doble igualdad agregada) no existe.
Pues bien, si, según reconoce Astarita, el agregado de los valores no coincide con el agregado de los precios de producción entre períodos (y aun cuando el tiempo de trabajo social no haya cambiado), ¿cómo podemos saber que la ley del valor sigue rigiendo bajo la forma de los precios de producción? Esto es, ¿cómo podemos saber que las relaciones de producción y de distribución dentro del capitalismo –regidas superficialmente por los precios de producción– están gobernadas en el fondo por la ley del valor y sólo por la ley del valor?
La respuesta que nos da Astarita en este punto es muy insuficiente: desde su punto de vista, si la ley del valor puede explicar “la formación de los precios de producción y de una tasa media de ganancia” (incluyendo la formación de nuevos precios de producción tras la aparición de un desequilibrio), entonces la ley del valor ha de ser válida. En sus propias palabras:
La teoría del valor trabajo es válida en la medida en que explica por qué y cómo se forman los precios de producción, y por qué y cómo se determina la tasa media de ganancia. Y, más esencial, explica por qué y cómo se genera la plusvalía (o la ganancia, interés, renta).
Que la ley del valor posea una explicación sobre cómo se conforman los precios de producción, incluso aunque superficialmente esa explicación sea compatible con las dinámicas que configuran socialmente los precios de producción (en realidad tampoco, tal como expongo exhaustivamente en el capítulo 5 del segundo tomo de Anti-Marx: pero no estamos debatiendo aquí sobre eso), no significa necesariamente que la ley del valor sea correcta: por ejemplo, la teoría del valor subjetivo también explica cómo se forman los precios de producción (los precios de equilibrio de las mercancías en un mercado competitivo capitalista) y también es superficialmente compatible con las dinámicas que configuran esos precios de producción. Pero Astarita no admitirá, meramente por eso, la validez de la teoría del valor subjetivo. Serán necesarios, pues, nuevos argumentos que acrediten la validez de la ley del valor: y aquí es donde Astarita pretende haber aportado cierta evidencia empírica. Cito:
La ley también explica la correlación entre la caída tendencial de los precios relativos de algunos productos y el hecho que pertenezcan a las ramas que han obtenido mayores avances de productividad. Marx consideraba que este era un test importante para la teoría del valor trabajo. He citado, con fin ilustrativo, datos de las estadísticas nacionales de EEUU.
Pero esta “evidencia” no es suficiente para validar la ley del valor por dos razones.
Primero, porque la ley del valor subjetivo también es perfectamente capaz de explicar que los aumentos en la productividad den lugar a caídas de precios (véase la sección final de este post de Álvaro Romaniega basado en Rothbard o, más simplemente, véase la propia ley de la utilidad marginal decreciente: a mayor oferta de una mercancía, menor es su valor marginal).
Segundo, porque podría suceder que la ley del valor explicara en parte la formación de los precios de producción pero no la totalidad de los mismos: a saber, que la ley del valor fuera condición necesaria para entender la formación de los precios de producción pero no condición suficiente. Recordemos que, para Marx, la ley del valor, y sólo la ley del valor, explica la formación de los precios de equilibrio (recalco que estoy hablando de precios de equilibrio, es decir, de precios de producción, no de precios comerciales o de mercado): pero con esto, Astarita sólo conseguiría demostrar como mucho que la ley del valor desempeña algún papel en la formación de esos precios de equilibrio, pero no un papel único. De hecho, que la suma de los valores no coincida con la suma de los precios de producción sugiere acaso intervengan otros factores en la determinación de esos precios de producción más allá de los valores. Tal como expongo en Anti-Marx (en el mismo apartado en el que aparece mi crítica a la solución de Moseley a la que Astarita está replicando):
El reto planteado por Bortkiewicz inflige un duro golpe a la teoría marxista: o bien los precios de producción no reflejan los valores o bien la ganancia no es la distribución de la plusvalía. O bien, por tanto, los precios de producción son algo distinto a una exteriorización de los valores, o bien el beneficio es algo distinto a una exteriorización de la plusvalía.
Al renunciar a solventar el problema de la transformación mediante las dos coordenadas que propugna Marx (doble igualdad agregada entre valores-precios de producción y plusvalías-ganancias), Astarita es incapaz de descartar que los precios de producción (y, por tanto, las relaciones de producción y de distribución dentro del capitalismo) dependan de otros factores distintos a la propia ley del valor.
En realidad, y como ya hemos explicado al comienzo, Astarita no renuncia totalmente a defender la doble igualdad agregada que postula Marx: lo que ha señalado reiteradamente a través de sus posts es que esta doble igualdad agregada prevalece dentro de un mismo período pero no entre períodos. Sucede que, en nuestro post anterior, ya demostramos numéricamente que esto no tiene por qué ser cierto. ¿Y qué tiene que decir Astarita frente a ello? Lo examinamos en el siguiente epígrafe.
La no respuesta de Astarita a la desigualdad entre valores y precios de producción dentro del mismo período de tiempo
Quizá la parte más decepcionante del último post de Astarita es que, en lugar de dar réplica a mis nuevas críticas, simplemente se dedica a esquivarlas para no afrontarlas. Como ya he explicado, en mi último post ilustro cómo las tablas de valores y de precios de producción de Moseley y Astarita pueden ser expresiones sociales de las relaciones físicas de producción de una economía productora de hierro, trigo y oro. De esa manera, demuestro que las tablas de Moseley y Astarita son compatibles con que el agregado de valores de una economía no cambie a lo largo del tiempo (ni tampoco su forma de expresión cuantitativa) y, sin embargo, la suma de los precios de producción sí lo haga. De ser así –y es perfectamente posible que sea así, tal como ilustro en mi ejemplo–, ni siquiera sería cierto que la igualdad entre la suma de valores y la suma de precios de producción se respete por necesidad dentro de cada período (y, por tanto, la débil solución al problema de la transformación de Moseley-Astarita se vendría abajo).
Por exponerlo una vez más (más detalles en mi post anterior). Empecemos con la tabla I, que contiene las relaciones físicas de producción):
La tabla I da lugar a la tabla II que contiene las relaciones de valor:
Y también da lugar a la tabla IV que da lugar a los precios de producción:
De tal manera que la suma de los valores (960 onzas) de la tabla II es igual a la suma de precios de producción (960 onzas) de la tabla IV. Pero si modificamos la tabla I, elevando los salarios, obtendremos la tabla VI (nuevas relaciones físicas de producción):
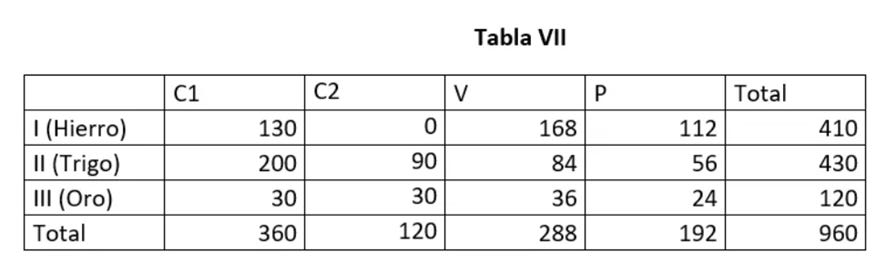
Que a su vez dará lugar a la tabla VII (relaciones de valor):
Y a las tablas VIII o IX (según se mantenga constante el valor añadido agregado o el valor del oro):
Podemos observar cómo la suma de los valores de la tabla VII (960) coincide con la suma de los valores de la tabla II (960), pero no coincide con la suma de los precios de producción ni de la tabla VIII (979,36) ni de la tabla IX (968,68). Por consiguiente, la suma de los valores no coincide con la suma de los precios de producción ni siquiera dentro de un mismo período de tiempo (el período de tiempo de la tabla VII y de las tablas VIII y IX es el mismo). A este respecto, la réplica de Astarita es entre pobre y nula.
Por un lado, a Astarita no le gusta que exprese la subida de salarios en especie en lugar de en términos monetarios (de 60 toneladas de trigo en la tabla I a 72 toneladas de trigo en la tabla VI) puesto que, a su juicio, el aumento de los salarios ha de ser monetario:
Rallo plantea que el aumento del 20% del salario equivale al aumento del 20% de las toneladas de trigo consumidas por los obreros (véase su tabla VI). Pero la realidad es que los salarios son abonados en dinero (onzas de oro en los ejemplos de Rallo), y no hay razón –dadas las variaciones de los precios de producción- para que ese aumento en términos de dinero se traduzca linealmente en un aumento de igual proporción de la cantidad de trigo (o una canasta de bienes salariales). Más en general, hay que tener en cuenta que el capital siempre se adelanta en la forma de dinero, no de mercancías.
Esta réplica no tiene ningún sentido, dado que, en mi mismo ejemplo, esa subida del salario en especie va de la mano de una subida del salario monetario (el capital variable pasa de 240 onzas en la tabla II a 288 onzas en la tabla VII). Que 288 onzas equivalgan dentro de mi ejemplo a 72 toneladas de trigo y que 240 onzas equivalgan a 60 toneladas de trigo es absolutamente irrelevante para la validez del ejemplo: en tanto en cuanto no haya ninguna contradicción en que 288 onzas sean equivalentes a 72 toneladas de trigo (y 240 onzas a 60 toneladas), el ejemplo es válido y debería ser compatible con la solución de Moseley. Por supuesto, podríamos recrear otro ejemplo en el que 288 onzas equivalieran a 60, 65 o 70 toneladas de trigo (como podríamos montar otro ejemplo en el que los salarios no subieran de 240 onzas a 288 sino de 240 a 250), pero estaríamos ante otro ejemplo. La cuestión es que, dentro del ejemplo que he expuesto, estas equivalencias son perfectamente válidas y, dadas estas equivalencias entre cantidades físicas y valores, la solución de Moseley y Astarita al problema de la transformación no se sostiene (en mi ejemplo, no existe igualdad agregada entre valores y precios de producción ni siquiera dentro de un mismo período).
Por otro lado, Astarita sigue empecinado en la idea de que mi crítica a Moseley consiste en rechazar su método secuencial para hallar el equilibrio:
Todo el argumento de Rallo (en Anti-Marx) para criticar la transformación de Moseley es afirmar que el desequilibrio de los precios entre sectores I y II invalida el método secuencial. En este respecto, es notable cómo Rallo se desliza sobre las dificultades. Como ya señalamos, en relación a la situación expresada en la tabla 2 no dice palabra sobre si en ella rige la ley del valor trabajo. Pero surgido el desequilibrio en la 3, plantea volver a Bortkiewicz. En ningún momento informa a sus lectores que basta aplicar el método secuencial para que, luego de un período de tiempo, se restablezca el equilibrio. He preguntado por qué no explicó esto; no tenemos respuesta.
He repetido en cada uno de mis posts que mi objeción no es al método secuencial de Moseley, sino a la solución de equilibrio final que arroja ese método secuencial (y que coincide, en su equilibrio final, con la solución que se desprende del método simultáneo de Bortkiewicz, tal como ya demostré aquí). Concretamente, y por repetirlo por enésima vez, el problema reside en que, en la solución final que nos ofrece Astarita con el método secuencial de Moseley (su tabla 9), la suma de los valores no coincide con la suma de los precios de producción: y no coincide no ya entre períodos sino que, como demostré en mi último post y he vuelto a repetir ahora, ni siquiera tiene por qué coincidir dentro de un mismo un mismo período (tabla VII frente a tablas VIII y IX). Frente a esto, Astarita no ha sido capaz de replicar nada. Sólo repite una y otra vez los mismos argumentos de sus posts anteriores que ya le han sido respondidos de todas las formas posibles y se niega a enfrentarse a los nuevos argumentos que se le han presentado. Por tanto, esta nueva réplica de Astarita no aporta sustancialmente nada nuevo.
Hasta aquí lo esencial de mi nueva respuesta a Astarita. Por resumirlo, una vez más: la resolución al problema de la transformación de Marx requiere que la suma de valores sea igual a la suma de precios de producción; Astarita sostiene que eso se cumple dentro de un período y no entre períodos de tiempo; en mi anterior contrarréplica le demostré, con sus mismas cifras, que esto no tendría por qué cumplirse ni siquiera dentro de un mismo período. No ha habido ninguna réplica a ello y, por tanto, la pelota sigue en su tejado: o replicar convincentemente o reconocer que la solución de Moseley es una mala solución (o callar si no es capaz de hacer lo primero y se niega a hacer lo segundo).
Antes de terminar, sin embargo, procedo a responder a ciertos comentarios accesorios (y no sustanciales) que efectúa Astarita a lo largo de su último post dado que él mismo se queja de que he dejado muchos de sus argumentos (no sustanciales) sin responder.
Adquisición de los inputs a precios de producción
De acuerdo con Moseley, la solución al problema de la transformación de Marx consiste en reconocer que los inputs se adquieren a los precios de producción y no a los valores. Desde mi punto de vista, y por lo explicado hasta el momento, esta propuesta no basta para solucionar el problema de la transformación. Cuando digo que “no basta”, obviamente me refiero a que no es suficiente: acaso sea condición necesaria para resolverlo, pero no suficiente. Extrañamente, Astarita intenta reconducir el debate a si la adquisición de los inputs a sus precios de producción es condición necesaria en lugar de suficiente:
Naturalmente, no es suficiente decir que a los precios de los insumos no hay que transformarlos en precios de producción. Sin embargo, la discusión que tengo con Rallo no es esa, sino si es, o no, una condición necesaria para explicar la formación de los precios de producción y de una tasa media de ganancia. (…) Pero además, ¿dónde afirmamos que es condición suficiente para explicar la formación de los precios de producción sostener que los capitalistas adquieren los insumos a precios de producción? Es obvio que “no basta” con esa afirmación.
Por mi parte, reitero lo evidente: me he limitado a afirmar que presuponer que los inputs se adquieren a sus precios de producción no es suficiente para solventar el problema de la transformación. Ni me importa si Astarita ha afirmado en algún momento que sea condición suficiente (si no ha pretendido afirmarlo, entonces la solución de Moseley al problema de la transformación es incompleta) ni tampoco es cierto que yo haya entrado a debatir en algún momento si es una condición necesaria (en realidad tampoco lo es, pues hay otras posibles soluciones al problema de la transformación que no parten de ese supuesto). Centremos el debate: como he expuesto más arriba, aun presuponiendo que los inputs se adquieren a sus precios de producción, el problema de la transformación sigue sin quedar resuelto (no se mantiene la doble igualdad agregada entre valores-precios de producción y plusvalía-ganancia ni siquiera dentro de un mismo período de tiempo).
Mi enfoque prescinde del tiempo
Aunque éste es un argumento que ya ha tratado más arriba, como Astarita lo repite recurrentemente, permítanme volver a aclararlo. Señala Astarita:
[El] enfoque básico [de Rallo] es que los equilibrios deben ser instantáneos, y el tiempo no cuenta. Lo afirma, de hecho, en este mismo pasaje: si aparece un desequilibrio, sostiene, los capitalistas pueden retroceder en el tiempo para cambiar lo hecho. Por caso, cuando ocurre un cambio en la tasa de explotación, los capitalistas deben “recalcular los nuevos precios de producción de los insumos”. Pero esto solo puede ocurrir “hacia adelante”, en una ronda siguiente, no en la que está teniendo lugar ahora. Es que una vez adquiridos los insumos a precios de producción, estos no pueden modificarse “hacia atrás” [negrita añadida]
En ningún momento he dicho que el equilibrio deba ser simultáneo porque, en caso de exponer una solución secuencial, ésta deba ser errónea. Y mucho menos he dicho (esto es pura invención de Astarita) que “los capitalistas pueden retroceder en el tiempo para cambiar lo hecho” (véase la negrita del párrafo anterior, que es, como digo, pura invención de Astarita que me atribuye como afirmación propia). Lo único que he dicho es que el equilibrio final de la solución simultánea y de la solución secuencia son el mismo equilibrio final (como ya demostré en este post anterior): por consiguiente, podemos limitarnos a exponer y analizar el equilibrio final sin necesidad de explicitar toda la secuencia de etapas que nos van acercando a ese equilibrio final. Si Astarita desea explicitarlo para ilustrar cuál es el proceso de reequilibrio, fantástico: pero lo que nos interesa es analizar si el equilibrio final cumple o no con ciertas propiedades (doble igualdad agregada) y, para ello, las etapas intermedias hasta alcanzar el equilibrio final no son relevantes (lo serán para entender el proceso de reequilibrio, pero no, repito, para analizar si el equilibrio final respeta o no ciertas condiciones).
Astarita dice no haber admitido que la doble igualdad agregada no sea alcanzable
Astarita ha repetido incesantemente que la doble igualdad agregada no se respeta en términos generales salvo dentro de un mismo período de tiempo. Extrañamente, Astarita me reprocha que yo exponga que ésa es su postura porque la suya es que la suma de salarios y plusvalía es igual a la suma de salarios y ganancias. En sus propias palabras:
Rallo me atribuye la idea de que si la suma de los valores es igual a la suma de los precios de producción, la suma de las plusvalías no puede ser igual a la suma de los beneficios. Sin embargo, cualquiera que lea mis respuestas anteriores puede comprobar que en todo momento sostuve que el valor agregado es igual a la suma de beneficios y salarios.
Recordemos lo que yo dije al respecto:
Es decir, que el propio Astarita admite que la única igualdad agregada que es capaz de mantener la solución de Moseley es “salarios agregados+plusvalía agregada” y “salarios agregados+ganancia agregada”. Pero ésa no es la igualdad agregada que exige Marx para resolver el problema de la transformación. Marx exige que C+V+P=C+V+G, a saber, que la totalidad del valor agregado (no sólo el valor añadido agregado) sea igual a los precios de producción agregados.
(…)
Sin embargo, Astarita trata de convencernos de que, aun cuando los nuevos precios de producción agregados no coincidan con los antiguos valores agregados entre distintos períodos de tiempo, éstos sí coinciden dentro del mismo período.
No veo entonces a qué viene el reproche. Si Astarita sostiene que el valor añadido es igual a la suma de beneficios y salarios (es decir, salarios+plusvalías=salarios+ganancias) y que, entre períodos de tiempo, la suma de los valores no es igual a la suma de los precios de producción, entonces es correcto atribuirle la idea de que la suma de valores no puede ser igual a la suma de precios de producción al mismo tiempo que la plusvalía agregada sea igual a la ganancia agregada (al menos, entre períodos distintos de tiempo). De hecho, Astarita vuelve a decirlo en este mismo escrito:
“Al interior” de las tablas 2, 3 y 9 se verifica que ∑ Pr Pr = C + VA = C + V + B. Esta igualdad no rige, sin embargo, en la transición hacia el nuevo equilibrio, como hemos visto en tabla 4.
O en su escrito anterior:
Las dos igualdades agregadas son satisfechas dentro de cada período porque, dentro de un período, cuanto más bajo sea C se reducen el precio-valor y los precios de producción por el mismo monto. Entre períodos la igualdad agregada de precio no será satisfecha porque C cambia entre períodos
No sé qué tergiversación me atribuye cuando expongo exactamente su postura.
Una aclaración terminológica: valor agregado y valor añadido
En realidad, este epígrafe no contiene una crítica a nada de lo relatado por Astarita sino una aclaración terminológica que puede haber generado confusión en ambas partes a lo largo de este debate. Cuando yo hablo de “valor agregado” me refiero a la suma de todos los valores o al agregado de valores: al valor total generado en la economía (C+V+S). Astarita usa en ocasiones el término “valor agregado” como sinónimo de “valor añadido”, es decir, como nuevo trabajo vivo añadido al trabajo muerto existente (V+S). De ahí que Astarita no entienda lo que yo le estaba replicando o que yo no entendiera en su momento lo que él estaba argumentando. En este párrafo se observa claramente la confusión:
No puedo entender por qué mi crítico afirma esto. En primer lugar, el valor agregado no es $960 sino $480. Los $480 del capital constante es valor agregado en etapas anteriores, que aquí reaparece como precio de producción con que los capitalistas adquirieron los insumos necesarios para la producción.
La suma de valores (valor agregado) es 960 onzas, mientras que el valor añadido agregado (la suma de salarios y plusvalía) es 480 onzas. En cualquier caso, el fondo del asunto no cambia: Astarita pretende zanjar el problema de la transformación diciendo que es suficiente con que el valor añadido agregado se mantenga constante entre períodos. Y no: si el agregado de valores se mantiene constante entre períodos, el agregado de precios de producción también debería hacerlo. Y no lo hace.
Intereses e ideología
Por último, Astarita necesita concluir su último post sugiriendo una especie de empecinamiento irracional, deshonesto o espurio por mi parte a la hora de criticar la teoría del valor trabajo:
Parece comprensible el empeño de un representante de la escuela austriaca en negar el carácter científico de la ley del valor trabajo de Marx. En el fondo, lo que está en juego es la crítica a una sociedad que se basa en la explotación del trabajo.
Parece que Astarita es incapaz de concebir que uno sea antimarxista porque los argumentos de Marx no le resulten persuasivos. A su entender, uno primero se posiciona antimarxista (por interés) y luego busca/retuerce los argumentos que necesita para avalar su posición. Y puede que haya muchos casos en los que sea así, pero no tiene por qué serlo así en todos los casos y, sea como fuere, no es relevante para el debate. Simétricamente, uno también podría decirle lo siguiente:
Parece comprensible el empeño de un representante de la escuela marxista en afirmar el carácter científico de la ley del valor trabajo de Marx. En el fondo, lo que está en juego es la crítica a una sociedad que ellos creen que se basa en la explotación del trabajo.
O simplemente, que Astarita lleva demasiado tiempo invertido en estudiar y divulgar el marxismo (con el consiguiente prestigio adquirido dentro de los círculos intelectuales de marxistas hispanohablantes) como para renegar ahora de la ley del valor. De ahí que necesite enredar, desenfocar y desviar el debate de sus aspectos centrales para no reconocer su error. Pero creo que no es necesario que nos enfanguemos en esto, puesto que no aporta nada al fondo del asunto: basta con que cada lector juzgue los argumentos presentados por cada cual y extraiga sus conclusiones al respecto.
Un resumen del debate
Entiendo que el debate se ha alargado demasiado por ambas partes y que pueda ser complicado de seguir. Para un resumen y una formalización del mismo, puede leerse este texto de Álvaro Romaniega.